Fermat's spiral

(description/explanation below)

First, try changing the seed angle.
Then click "loop through angles" to automatically change the seed angle by small increments.
Then click "fade discs" to see pretty things happen.

created by Anita Lillie

I originally built this in Processing/Java (source) but have since converted it to Processing.js/JavaScript (you can view source in the browser).

What is Fermat's spiral?

Fermat's spiral is a special kind of spiral defined by this polar equation: r = ∓√Θ,
where r is the radius and Θ is the angle about the center (usually measured from directly rightward).

This just means that, as you move out from the center, you shift around by an amount proportional to the square of the amount you moved out. Since the square of a number is slow to increase at first, but gets faster and faster as the number increases, the spiral loops around slowly at first, then gets tighter and tighter.

Here's one half of Fermat's spiral (the positive half of the equation above):

You can display this curve in the tool above by selecting these parameters:

Placing dots along the spiral

Something interesting happens when you start laying out dots at regular angular intervals as you move around the spiral. This is what the tool above does. If you choose a very small angle, like 1° in the example above, you plop down dots very frequently, and basically you get to see the whole spiral's shape. But imagine that you plopped out dots less frequently, for example, only every 90°. Then you would only see dots any time the spiral crossed 0°, 90°, 180°, and 270° (which gives you something that looks like a plus-sign):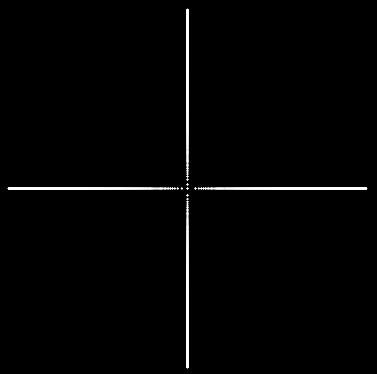

Similarly, a seed angle of 180° will only give you dots along a horizontal line.

And this is just the beginning! It's really fun to experiment with different seed angles for Fermat's spiral, because you get some very nice patterns.

Irrational numbers can give some of the most intriguing patterns. Selecting the golden angle (which we approximate here as 137.5°), results in very evenly spaced, and therefore well-packed, dots. This is the very same pattern that you see in disc phyllotaxis in sunflowers and daisies, the arrangement of seeds in the center of the flower. (See this article for a deeper discussion of this and other irrational numbers as seeds for the spiral.)

The tool on this page

I built this applet so that anyone can play with the seed angles for these patterns, and create some hypnotizing visuals in the process.

Here's a brief explanation of some of the parameters you can play with:

"seed angle"
This is the regular angular interval at which to drop dots, as you move out from the center of the spiral.

"go to golden angle"
Snaps to the golden angle (approximated here as 137.5°).

"loop through angles?"
This button toggles looping, which starts with the seed angle, steps by the "looping angle step size" defined below it, at a rate defined by "looping frame rate".

"fade discs?"
This button toggles fading, which makes each disc fade from white to black, and back again, at a rate proportional to its disc number. (Discs are numbered outward from center of spiral.) Adjust these by setting the fade rate of both the "innermost" disc and the "outermost" disc. Fading discs in this manner was inspired by the wonderful postings of KrazyDad.

"disc size range"
Each disc is size according to its disc number. (Discs are numbered outward from center of spiral.) Adjust size range by setting the diameters of the "innermost" and "outermost" discs.

One of my excuses for making this was to introduce myself to Processing. If you're learning too, or just curious, please feel free to look at the source code.

Related links

Feedback?

Post a comment to my blog

Last updated 2007-07-19

© 2007, Anita Lillie